Discretization

Let \(f = \left\{\begin{array}{ccc}\{t_k,k\in\{1,\cdots,n\}\} & \longrightarrow & \mathbb{R}_+ \\ t_k & \mapsto & f(t_k) \end{array}\right.\), a function representing load or production as a function of time.

We define the discrete charge monotone of the function \(f\) as follows:

\[\begin{split}C(f) : = \left\{\begin{array}{ccc} \mathbb{R}_+ & \longrightarrow & [0,T] \\ x & \mapsto & \sum_{k|f(t_k)\geq x} \delta_k \end{array}\right.\end{split}\]

The figure bellow shows an example of time and power normalized duration load from a discrete time series

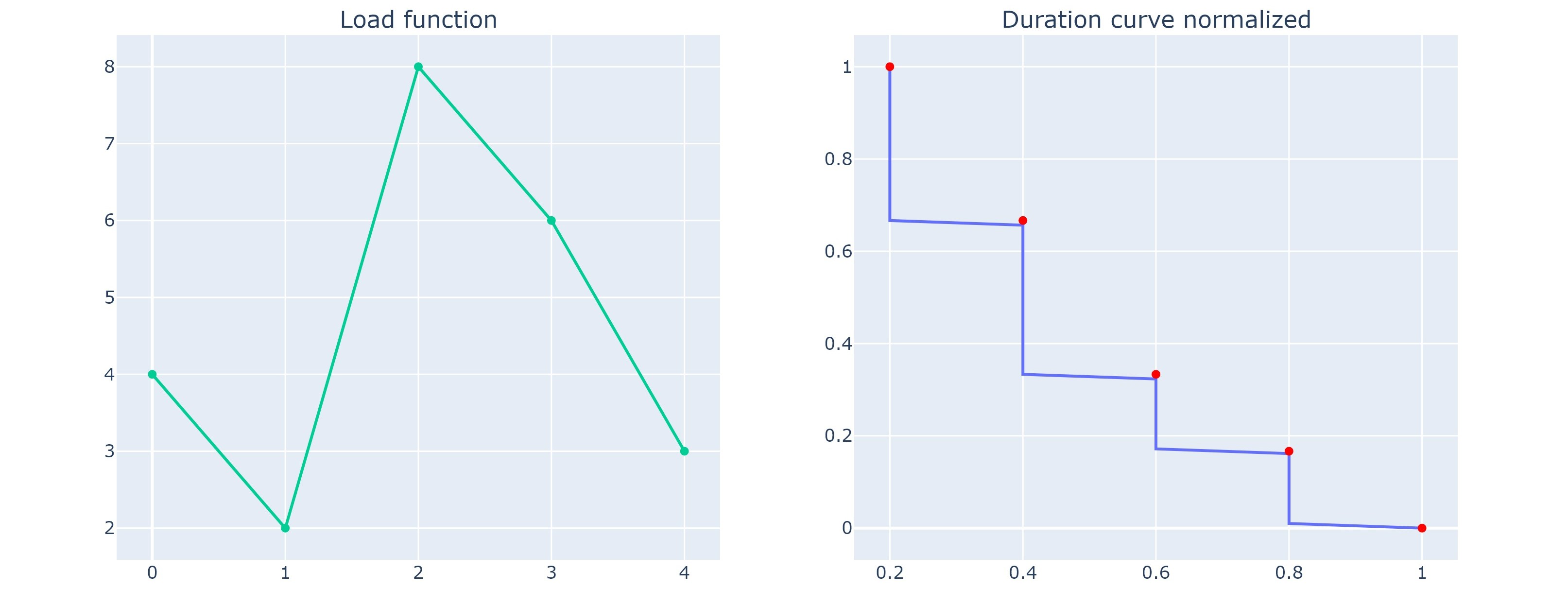
Note

The maximum (value 1) is reached 20% of the time because a point represents a non-zero time range. The left curve should instead be represented by steps.

Where \(\delta_k\) represents the duration associated with instant \(t_k\) and \(T=\sum_{k=1}^n\delta_k\) represents the total duration covered by the function. This notation makes it possible to cover the case where a value given by the load function does not correspond to the same duration.

In the case where each \(t_k\) represents a uniform duration (which we denote \(\Delta\)), we then have the simplification:

\[\begin{split}C(f) : = \left\{\begin{array}{ccc} \mathbb{R}_+ & \longrightarrow & [0,T] \\ x & \mapsto & |\{k|f(t_k)\geq x\}| * \Delta \end{array}\right.\end{split}\]

Normalization

Power normalization follows the same logic as continous cas.

For time normalization we set :

\[\begin{split}\tilde{C}(f) = \left\{\begin{array}{ccc} \mathbb{R}_+ & \longrightarrow & [0,1] \\ x & \mapsto & \frac{C(f)(x)-C(f)_{min}}{C(f)_{max}-C(f)_{min}} = \frac{\sum_{k|f(t_k)\geq x} \delta_k}{T} \end{array}\right. \text{ où } \left.\begin{array}{l} C(f)_{min} = \underset{x\in\mathbb{R}_+}{\text{min }} C(f)(x) \\ C(f)_{max} = \underset{x\in\mathbb{R}_+}{\text{max }} C(f)(x) \end{array}\right.\end{split}\]

Uniform case :

\[\begin{split}\tilde{C}(f) = \left\{\begin{array}{ccc} \mathbb{R}_+ & \longrightarrow & [0,1] \\ x & \mapsto & \frac{|\{k|f(t_k)\geq x\}|}{n} \end{array}\right.\end{split}\]